今回は”倍音”について解説します。
“周波数“同様、倍音はEQ(イコライジング)を行う上で重要なポイントとなります。
概要
・”倍音とは何か”を理解する
・楽器(音源)が持つ倍音の聴こえ方を意識し、効果的なEQを行うための基礎を学ぶ
倍音とは
倍音とは、楽器を演奏した時に発する音程(基音)に対して2以上の整数倍で鳴っている音の事です。
人の声や音を奏でる楽器のほとんどはこの倍音を持っていて、目立つ/目立たないはありますが、実際に演奏する基音に対して2~3オクターブ上の音までが混ざって出ています。
※ちなみに、倍音は読んで字のごとく、下には存在しません。
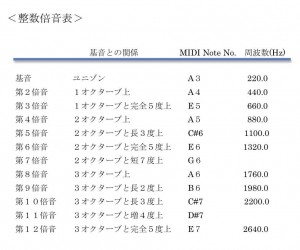
以下、整数倍音表(注1)を見てみましょう。
表を見てもわかるように、第4倍音までは協和音(注2)ですが、それ以降には不協和音も混在してきます。
特に第9倍音以降はとても厳しい不協和音がなってしまうことになりますが、この辺りは聴感上ほとんど気にならない部分です。
上記の整数倍音表は音程を持つ楽器の倍音列を記載していますが、ドラムなどの打楽器は少し特殊です。
整数倍の倍音ではなく、不規則な非整数倍音が生じます。
この倍音の聴こえ方が、楽器固有の音色を作り出しているということを理解しましょう。
また、EQの基本は、実は基音を処理するよりも倍音を整理することが重要であることも覚えておきましょう。
(注1):整数倍音表 上記周波数は純正律での計算のため、ピアノロールの基音対応表(平均律)の周波数とは若干の差が出てきます。 この「純正律」と「平均律」について興味のある方は、個別に調べてみて下さい。
(注2):協和音 協和音とは完全5度とオクターブの音程のことを指し、それ以外の音程は全て不協和音となります。
倍音のイコライジング
ギターとピアノを例にして、説明を進めましょう。
まず、ギターで演奏可能な基音、6弦の開放音(E2)から1弦12フレット(E5)までの3オクターブがどのくらいの周波数になるか想像してみましょう。
冒頭の基音対応表にあてはめてみると、
6弦開放(E2) = 82.407Hz
1弦12フレット(E5) = 659.26Hz
となっています。
みなさんの予想よりもだいぶ低かったのではないでしょうか。
ここからEQへ話が移りますが、ギターといえば我々プロのエンジニアもまずは中域1.5KHz~3KHzぐらいを意識してブーストすることが多いです。
しかし、この辺りは実際には基音ではなく、倍音に相当する部分を処理しているということになります。
なぜこの部分をEQするかというと、基音が他の楽器でマスキングされて聴こえないような場合に、倍音をEQすることで基音を感じさせているのです。
例えば、ギターがオケに埋もれて見えなくなっているような場合に、倍音領域をブーストして音が抜けるという状態になります。
また、ピアノの場合、最高音(C8)は4KHz強であるにも関わらず、実際にはその4倍にあたる16KHzをEQすることもあります。
(デジタルの世界では20KHzまでのサンプリング/再生能力を持っているため)
つまり、実音的には存在が難しい超高域にも”倍音”というものが存在しているということです。
倍音をEQしているケースは上記のような場合が多いですが、当然のことながら基音である低域~中低域を無視することはできません。
楽曲の中では、ほどんどの楽器やボーカルの基音は100Hz~700Hz辺りに集中しているので、「どの楽器がメインなのか」をしっかり踏まえて音を作っていく(EQする)必要があるということも理解しておきましょう。
楽器の持つ倍音
次は、楽器から発せられる倍音を確認していきましょう。
下記画像は、バイオリンがミドルA(440Hz)を演奏した時のアナライザー画像です。
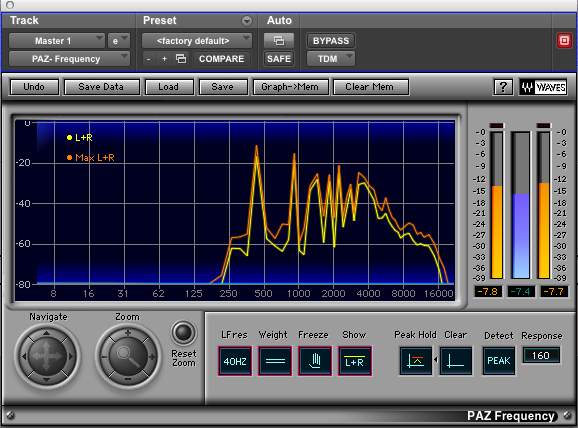
基音の440Hzが1番大きく振れ、次に第2倍音の880Hz、第3倍音の1,320Hzと第4倍音の1,760Hz辺りは一緒に鳴っているような感じですが、理論的に言われているポイントのレベルはだんだん落ちるように存在しているのが分かりますね。
それでは、このバイオリンの倍音がどういうものなのかを動画で確認してみましょう。
①バイオリンがミドルA(440Hz)の音程を弾いた時の音をそのまま再生
②EQで440Hzの前後を鋭くカットして再生
④440Hzの正弦波をオシレーターでならしているものを再生
まとめ
いかがでしょうか。
バイオリンの倍音がどういうものなのか、感じることができたのではないでしょうか。
倍音の豊かなバイオリンから倍音をEQでカットしてしまうと、味気のない③の正弦波のようになってしまうのです。
このように、楽器のほとんどには”倍音”が存在しています。
今回は分かりやすく単音の例を出しましたが、コードトーンになると、かなり複雑な倍音構成になった和音が形成されます。
ですが、算数のように計算する必要なんて全くありません。
楽器というのは、こういうものが必ず一緒に鳴っているのだということを理解しつつ、その楽曲やコードトーンにとって邪魔なポイントに敏感になることが、重要なポイントなのです。
![周波数を理解する [動画あり]](http://fl-mixingroom.com/wp-content/uploads/2015/10/eyechatch_mix-150x150.png)